How to solve a Sudoku puzzle? (Part 2 of 4)

[This post is a part of the main post - Sudoku Solver with GUI written in python.]

This post explains the 'logic' required to solve Sudoku puzzles.

(These are also exactly the same steps I have followed in my program, Sudoku Solver, to solve Sudoku puzzles.)

Sudoku rules -

The objective of a Sudoku puzzle is to enter a number from 1-9 in each cell, in such a way that:

• Each (horizontal) row contains each number exactly once.
• Each (vertical) column contains each number exactly once.
• Each of the 9* 3x3 boxes (or subgrids) contain each number exactly once.

(* - not any 3x3 box. More info here.)

Steps involved in solving Sudoku puzzles -

(Note: The steps described below are the steps I have followed in my program to solve Sudoku puzzles. There can be more ways to do the same.)

(If you are trying to understand the logic.py module (here) -
In the examples below, I have provided the name of the function (ie either Step1 or Stepk) in square brackets which contains the logic to solve that example,.)

Lets go through some easy steps first.

In the very first approach, we will try to solve the puzzle 'exactly' as far as possible. This is the simplest approach and the puzzle won't be significantly solved in most cases.

Rule #1:
If there is only 1 permissible number in a cell, enter that number in the cell.
(Permissible numbers are those numbers which you can enter in the cell without immediately violating the Sudoku rules. The rules may later get violated.)

Example #1 [Step1 (algorithm 1)]

In a row, since the only numbers can be 1 - 9 and none can repeat, it is clear that, in the picture below, the only permissible number in the cell (2,5) {row 2, column 5} is '5'.

(Puzzle #1)

Example #2 [Step1 (algorithm 1)]

Similarly, in a column, since the only numbers can be 1 - 9 and none can repeat, it is clear that, in the picture below, the only permissible number in the cell (5,7) {row 5, column 7} is '5'.

(Puzzle #2)

Example #3 [Step1 (algorithm 1)]

Similarly, in a box, since the only numbers can be 1 - 9 and none can repeat, it is clear that, in the picture below, the only permissible number in cell (2,2) {row 2, column 2} is '5'.

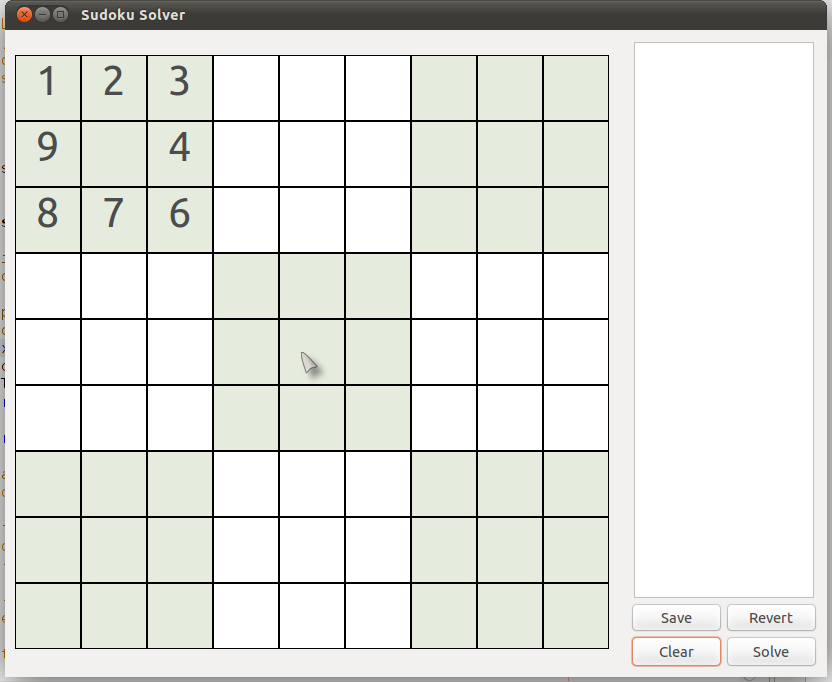(Puzzle #3)

(There can be more examples based on the same rule.)

Lets proceed 1 step further.

Even in the next approach, we will try to solve the puzzle 'exactly' as far as possible. However, this is not easily visible on the very first glance. Nevertheless, it is still easy!

Rule #2:
If a number is permissible in only one of the cells in a row, then enter that number in that cell. That cell may then have more permissible numbers. Similarly, for column and box. (Below is an example for a box.)

Example #4 [Step1 (algorithm 2)]

Have a look at the puzzle below. Try to analyse the cell (2,8) {row 2, column 8}.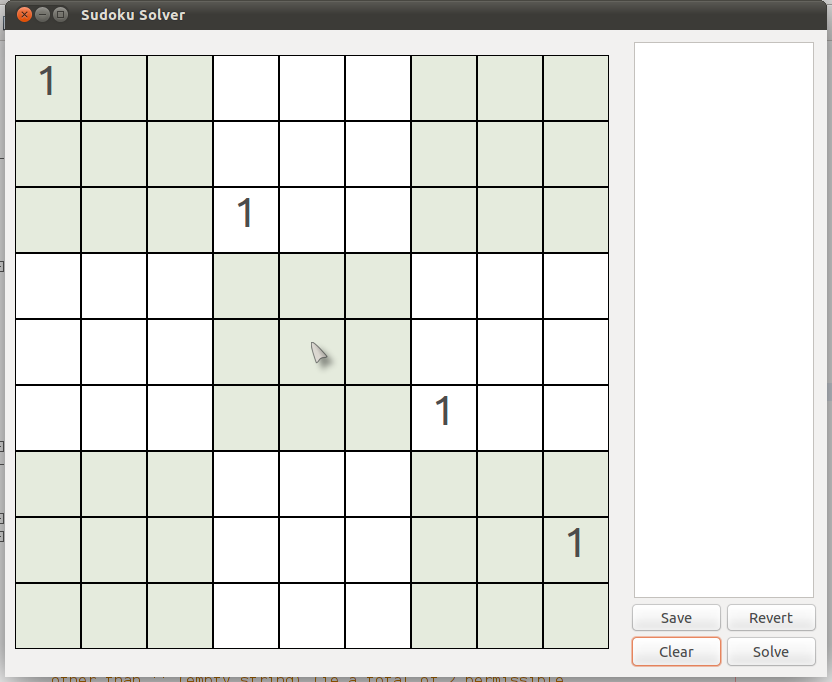

(Puzzle #4)

You will find that all numbers 1 through 9 are permissible for that cell. However, if you look carefully, you will find that it is the only cell in its box which can hold the number 1. Hence, we can be absolutely sure that the number in this cell should be 1.

(There can be more examples based on the same rule.)

You can practise some 'easy' level examples here to memorize the above 2 approaches.

Now, for something difficult.
Until now we solved everything 'exactly'. However, in most situations these approaches alone cannot take us much far. What we have to resort to then is assumptions! This is an approach with the help of which you can solve any Sudoku puzzle. It is like a universal tool (रामबाण).

Rule #3:
When unable to solve any further using the above approaches, make an assumption, and then try to solve it further using the above approaches. If at some point Sudoku rules get violated, then it implies that your assumption was incorrect. If so, revert back to the point where you took the assumption, take the other assumption (on the same cell) and again proceed further as before. Otherwise, if you don't encounter any rule violations till the end, your assumption was correct (and you got lucky!).
This will be more clear from the example below.

(Note: This approach is not actually difficult in the true sense, it is just laborious. Hence it is better to use this after Rule #1 and Rule #2. However, you can always this before Rules 1 and 2 if you want to!)

Example #5 [Stepk (AssumptionLevel 1)]
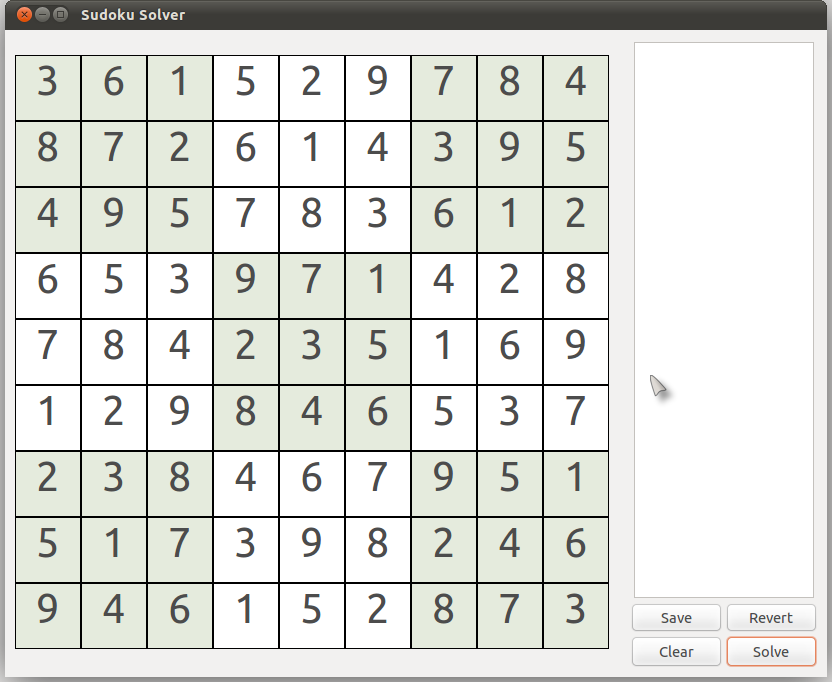
Observe the puzzle below. Let us try to solve this using Rule #3. Observe the cell (7,8) {row 7, column 8}.

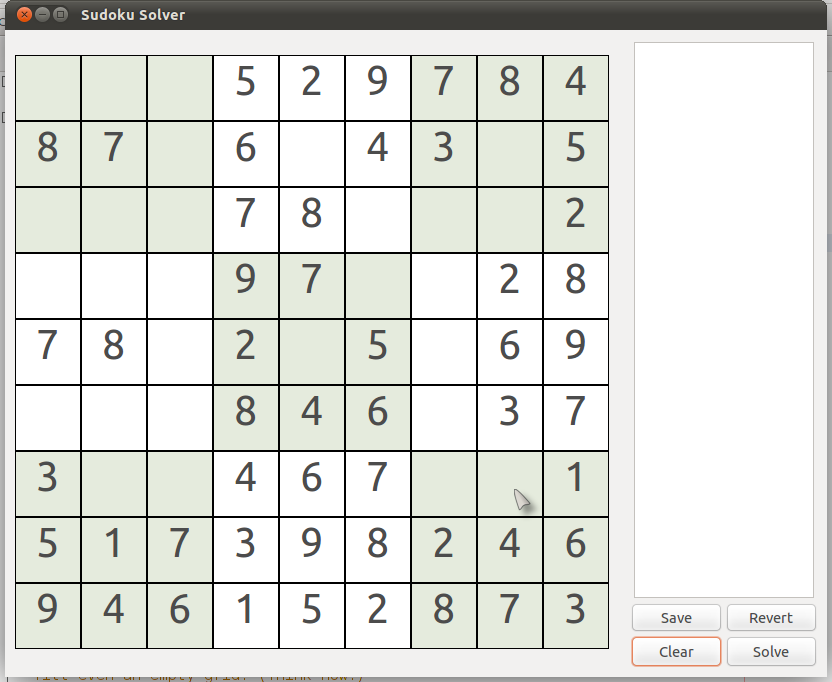(Puzzle #5)

You may notice that, for now, the only permissible numbers in that cell are 5 and 9. We cannot directly say at this point which one is correct (but only among them is correct!). This is where we decide to take an assumption. Let us assume the number 9 in that cell.

Now we will try to solve it further using our first 2 'exact' approaches. It can be immediately seen that, using Rule #2, the number in cell (3,7) {row 3, column 7} should be 9.

Similarly, again using Rule #2, the number in cell (2,3) {row 2, column 3} should be (again) 9.

Now, if you look carefully, you will find that there is some problem. You cannot fit 9 anywhere in the box (2,1) without violating the Sudoku rules. But this itself is a violation of the 3rd rule - "Each of the 9 3 x 3 boxes (or subgrids) contain each number exactly once." But where did we go wrong?

 - at the point of assumption! We wrongly assumed the number in the cell (7,8) {row 7, column 8} (in Puzzle #5) to be 9. Although we were not sure about it then, we can now be sure that the number in the cell (7,8) {row 7, column 8} in Puzzle #5 should be 5!
(Note: This is the reason why we made an assumption on a cell which then had only 2 permissible numbers. Had we made an assumption on some other cell which had more than 2 permissible numbers, we would have not been able to deduce the correct number even at this stage!)



Now that we have the correct number in cell (7,8) {row 7, column 8}, we try to solve it further using Rules 1 and 2. You will notice that the puzzle now easily gets completely solved.

This might take some time to understand. You can practise some 'medium' level examples here to better understand this approach.

There still remains 1 unanswered question -

How to decide on which cell an assumption must be made?
You can make an assumption on any cell as long as it has only exactly 2 permissible numbers. It is quite possible that you may not be able to make a decision (about the correct number in a cell) on the very first assumption itself (and this is what usually happens), where both the assumptions (on that particular cell) might seem to be true. In this case, you need to leave that cell and try for an assumption on some other cell.

The True Picture -
     99.9% of the Sudoku puzzles can be solved using this approach. For the rest 0.1% you need to resort to assumptions over assumptions. This is again not difficult, but it becomes too laborious and should be kept as a measure of last resort after you have tried to solve the puzzle by making assumptions on all cells (with exactly 2 permissible numbers) and still you are not able to solve the puzzle completely.
     Don't worry, you normally won't come across any puzzle from this 0.1% category!
(Not even the hard/extreme/evil Sudoku puzzles on most websites fall in this category!)

     I denote the nesting of assumptions by their level. In the above puzzle #5, we made only 1 assumption and solved the rest of the puzzle exactly (ie using no more assumptions.) This assumption is denoted as an assumption of Level 1. If you are taking an assumption on an assumption (and no more assumptions), the later assumption is an assumption of Level 2. Similarly there can be more levels.


Remember the link to one of the toughest puzzles I gave at the beginning of the main post? (if not, it is here).
To solve it completely, it requires an assumption of Level 3!